CHORDS

Thus far, we’ve discussed individual pitches (in Units 3, 5, and 6), and pairs of pitches and the intervals they form (in Unit 7). The following videos review the operative concepts:

 

This unit will examine combinations of three or more pitches as they form chords.

Chords

Two pitches can combine to form an interval. Three or more pitches can combine to form what musicians call a CHORD. Some musicians feel that only certain three- and four-note groups constitute chords. Others feel that some chords can be formed even by five or more pitches. We’ll investigate three- and four-note chords in this unit, and touch on the idea of extending chords with more pitches. In Western tonal music, not every combination of three or more pitches forms a chord. In fact, what we consider to be a chord is based on some narrow restrictions, stemming from acoustic principles and cultural practices. We’ll begin by investigating the simplest of chords — triads.

Triads as Stacks of Thirds

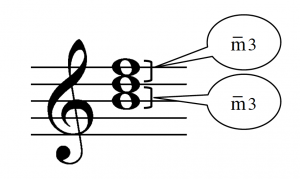
Triads may be thought of as generated by stacking two thirds atop one another. For example:

The Members of a Triad

Root, Third, and Fifth When triads are viewed as a stack of thirds, the lowest pitch is the ROOT. The pitch a third above the root is called the THIRD, and the pitch a fifth above the root is called the FIFTH:

 

Triad Qualities

To begin with, let’s build triads by using only the pitches in a single major key. We can build a triad on each scale degree in a major scale, using only the pitches from the key of that scale:

Let’s now investigate the structure of these triads by examining the thirds they comprise. The first consists of a major third surmounted by a minor third:

But the second has a minor third surmounted by a major one:

This gives us two different types of triads. The first is called a MAJOR TRIAD; the second is called a MINOR TRIAD.

If you examine the remaining triads, you’ll notice that they are all either major or minor triads, except for one:

This triad consists of two minor thirds. We call this a DIMINISHED TRIAD. And there is one more type of triad, which can’t be constructed from the diatonic pitches in a single key, but which is nonetheless important to know. If we stack two major triads atop one another, the result is an AUGMENTED TRIAD.

To determine the quality of a triad, identify the qualities of its two component thirds (from root to third, and from third to fifth), and compare to the triad quality definitions above. For example, consider the following triad:

The interval from root to third (F sharp to A) is a minor 3rd. The interval from third to fifth (A to C sharp) is a M3. Therefore, this is a minor triad.

 

Naming Triads

We name triads by their roots. There are two common ways to do this: one uses the letter name of the root; the other uses a Roman numeral to label the scale degree of the root within a key.

We can name a triad by stating the letter name of its root, followed by the quality of the triad. Here’s an example of a B-flat major triad:

The root of that triad is B flat. And because it consists of a major third surmounted by a minor third, the quality of that triad is major. Therefore, we may call it a Bf major triad. Some musicians use symbols to represent each triad’s quality. This kind of system is used widely among jazz, rock, and pop musicians, but the symbols vary quite widely. Here are the four types of triads, each built on C, and some of the more common pop/jazz chord symbols used to represent them:

We can also name a triad by using a Roman numeral to represent the scale degree of its root. For example, look at the chord formed by the pitches in m. 5 of the following folk song:

Those pitches (A flat – C – E flat) form a major triad with a root of A flat — the 4th scale degree in the key of E flat major. Therefore, we use the Roman numeral › to label this chord in this context:

                                                                                    E flat: IV

This kind of labeling requires the context of a prevailing key. You must be sure to identify the tonic of the surrounding music and write that down before any Roman numerals you write. You should write the tonic once, followed by a colon, at the beginning of a passage before you write any Roman numerals to identify chords. For example:

                                                           B major: I           IV          V           I

We can use upper-case and lower-case Roman numerals to distinguish between major and minor chords.

                                                         F major:       I                         ii

We represent diminished triads by adding a superscript circle to the right of a lower-case Roman numeral. We represent augmented triads by adding a superscript plus sign to the right of an upper-case Roman numeral.

                                                              C minor:           viio             V+

 

Inverting Triads

In most Western music, the lowest pitch in a chord is especially important because it supports and governs the pitches above it. We refer to that lowest pitch as “the bass,” and we say that a pitch or member of the chord is “in the bass.” For example, in referring to the very first triad we examined at the beginning of this chapter, we could say “the bass is C” or “C is in the bass.” We could also say that the root of the chord is in the bass.

Triads don’t always appear with their roots in bass. In fact, many times the third of a triad will show up in the bass. Thus, we might find the same C-major triad not with C (the root) in the bass, but with E (the third) in the bass:

That chord is still made up of the pitches of the C-major triad, but those pitches have been rearranged so that a different member of the chord is in the bass. When this happens, we say that the triad has been INVERTED. If the root of a chord is in the bass, we say the chord is in ROOT POSITION. If the third of a chord is in the bass, we say the chord is in FIRST INVERSION. If the fifth of a chord is in the bass, we say the chord is in SECOND INVERSION. It’s important to note the intervals above the bass (not the root) formed by each inversion. In root position triads, the other two chord members form a fifth and third above the bass. (These might appear in higher octaves, but we still refer to the intervals they form as fifths and thirds.) We say that this triad is in 5 3 (“five-three”) position.

In a first-inversion triad, the other two chord members form a sixth and third above the bass, and we can also say that the triad is in 6 3 (“six-three”) position.

And in second inversion, the other two chord members form a sixth and fourth above the bass, and we can also say that the triad is in 6 4 (“six-four”) position.

In Western music, most triads appear frequently in root position or first inversion. Second inversion triads — because of the prominence of the dissonant fourth above the bass — are usually reserved for special uses.1

In classical music theory, we combine a Roman numeral that represents the root (not the bass) of a triad with Arabic numerals, called FIGURED BASS, to indicate the intervals above the bass in inverted chords.2 If a triad is in root position (with a fifth and third above the bass), we write only the Roman numeral. A Roman numeral without figured bass represents a root-position chord:

                                                                         D major:         V

For triads in first inversion, we write “6” (as shorthand for 6/3):

                                                                             D major:     V6

And for triads in second inversion, we write “6/4.”

                                                                             D major:     V6/4

Pop, rock, and jazz musicians represent inverted chords by drawing a line under the chord symbol, then writing the letter name of the pitch in the bass. For example:

 

 

Constructing Triads

You may be given certain sets of criteria on which you must construct triads. In general, you’ll be given a root, a quality, and an inversion. This might come it one of several forms. For example: Write a B-major triad in first inversion:

Chord Spacing & Doubling

Thus far, we’ve been looking at only the simplest incarnations of triads — three pitches spaced closely together. However, triads appear in all kinds of spacing (also called “voicing”). For example, the pitches in a triad need not be spaced closely together:

And it is possible to double members of a triad at various octaves as well:

Different doublings and spacings change the texture (see Unit 15) of a chord (and hence some of its affect), but they do not alter its root, quality, and inversion. For example, the following are all E major triads in first-inversion:

Melodic Expression of Chords

Although certain instruments (such as the piano and guitar) are particularly adept at sounding chords by producing multiple pitches simultaneously (and groups of instruments together can create the same effect), even instruments and voices producing one pitch at a time can render chords by ARPEGGIATING through some or all of the pitches of each chord in succession. ARPEGGIATION is the process of horizontally unfolding the pitches of a chord. The first example arpeggiates an E major triad– note that every single note is part of an E major triad:

 

The next example is in G major, and first arpeggiates a I chord (a G major triad in the key of G major) and then a V chord (a D major triad in the key of G)

Finally, the next example arpeggiates three triads in D major. First a tonic (I) chord, then a IV chord, then returns to a I chord.